Constructing the Centroid.

This is a geometric concept that entails constructing a median, the middle point of the center of a segment that is equidistant, in each given segment of the triangle. From the midpoint, there is a segment then constructed that directly connects from the opposite vertex of the addressed segment; consequently, all three newly created segments then intersect at the middle of the triangle.

 

 

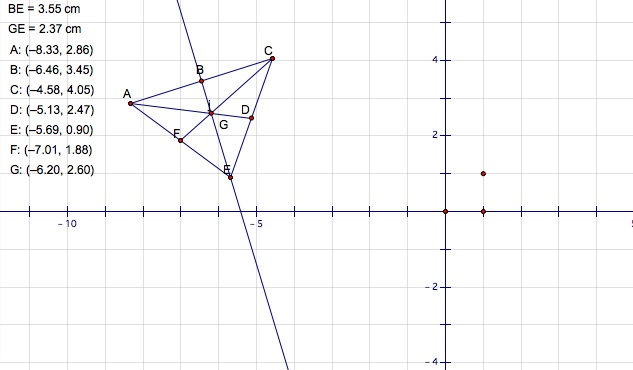
In a classroom setting, students will be introduced to what is the centroid of a triangle and how to sketch on the geometry sketch pad. Students will examine the relationships of the median of the given segments in a triangle and how it directly relates to the centroid of the triangle. Students will discover that the centroid is a point of concurrency in a triangle as there are three intersecting lines constructed from each given median of the triangle.

 

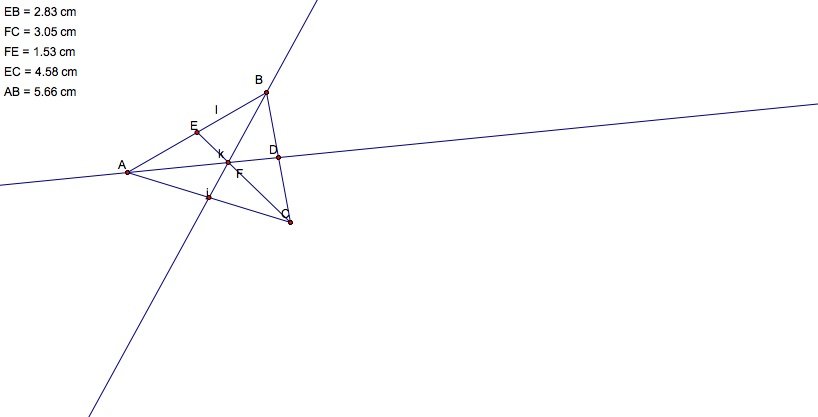
 Students will explore and conclude that distance from the centroid to the median of each respect segment of the triangle is 2/3 of the segment connecting from the median to the opposite vertex. Students will manipulate the sketch pad and add grid in order to localize points of each segments.

 

 

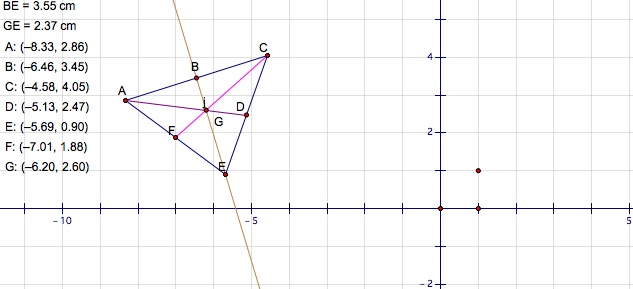
Students will use the formula to calculate the midpoint algebraically and compare it to the given coordinates of the sketch on the sketchpad, m = (x₁ +x₂)/2, (y₁+y₂)/2. In addition, students will explore the distance formula of square root [(x₂-x₁)² + (y₂-y₁)²]. With the distance formula, we will be able to prove that the centroid is indeed 2/3 the distance from the vertex to the midpoint of the opposite vertex.

 

 

Students should thoroughly enjoy this assignment as they are exploring the measuring geometrically and algebraically. Students should be able to demonstrate the distance from centroid to the selected vertex, using the distance formula equates 2/3 of the segment from the midpoint to the opposite vertex.